Why carbon nanotubes are stronger than steel?
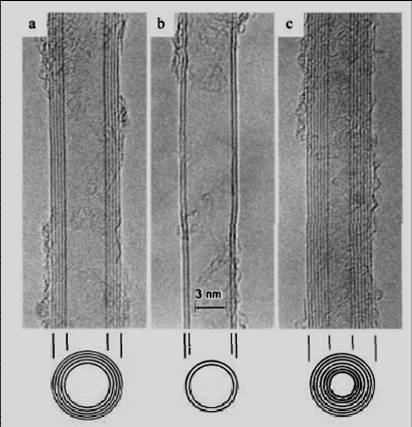
A carbon nanotube is a giant molecule of carbon atoms which has a cylindrical framework (tube) with a radius of about a nanometer. This is where its name comes from. Nanotubes can be inserted one into another, and then they are called multilayered. It is only possible to see nanotubes with the help of an electron or scanning probe microscope. Below are images of multilayered nanotubes obtained with the help of an electron microscope S. Iijima(Nature 354, 56, 1991). On the left are images of cross-sections of five layer (a), two layer (b) and seven layer (c) nanotubes. On the right are images of a cross-section of a nine layer nanotube with internal diameter of a 10 nm.
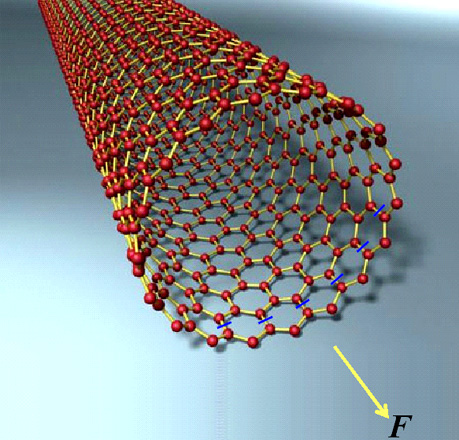
Experiments have measured the tensile strength of carbon nanotubes to be very high, around 60 GPa. Whereas steel's strength is around 0.8 GPa. Why is it that nanotubes are almost a hundred times stronger than steel? Let's try to calculate the strength of a single-walled nanotube, like the one shown below. One third of the C-C bonds of such a nanotube are oriented along the axis of the nanotube itself. Let's secure the invisible end of a nanotube and apply a tensile force F to the other end of it. Carbon atoms are indicated by red balls; covalent bonds between these atoms are indicated by yellow lines. Blue line segments strike through C-C bonds which are directed along the axis of the nanotube, and a yellow arrow shows the direction of tensile force F.
Let's assume that carbon atoms in a nanotube form identical bonds between each other (C-C, σ-bonds), and the angle between them equals 120°. Then when stretching a nanotube these bonds will stretch identically. However a nanotube can break in a very intricate and fanciful ways depending, for example, on which C-C bond breaks first. To simplify our calculations let us assume that the force will break only C-C bonds that are directed along the axis of the tube and located in the same plane of the cross-section. It is known that the distance d between the nearest carbon atoms in a nanotube equals approximately d = 0.15 nm. It is easy to show that if the tube's diameter equals D, then the amount N of bonds directed along the axis of the tube equals:
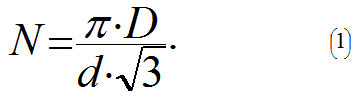
Besides, a force applied to every C-C bond which is equal to F/N
What does the strength of one C-C bond equal?
One can find out the strength of a C-C bond using a dependence of energy on distance between the atoms. The potential energy of a mole (i.e. 6 x 1023) of C-C bonds (U, in kJ/mole) correlates to the distance between the nuclei (r, in pm) as shown below.
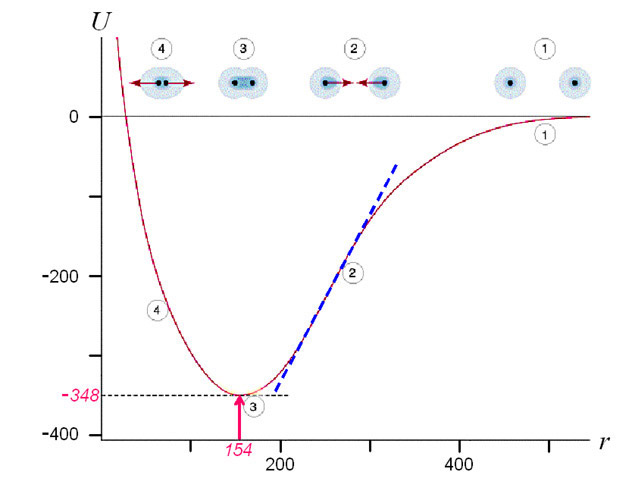
It follows from the diagram above that the potential energy of a bond reaches its minimum when the distance between the nuclei of the atoms is 154 pm (1 nm = 1000 pm). This is what determines the distance at which carbon atoms are located in a non-stretched nanotube. The tangent of the line slope of the right part of the curve in diagram is proportional to force F1 which is needed to keep atoms at the distance r:
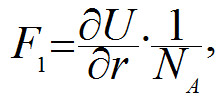
where NA is an Avogadro constant, 6x1023 mole-1. In order to increase the distance between the carbon atoms one needs to apply force F1, and if this force is more than the maximum tangent of the slope angle (see blue dotted line in the diagram above) then the C-C bond will break. This is why the following formula will determine the force at which the bond will break
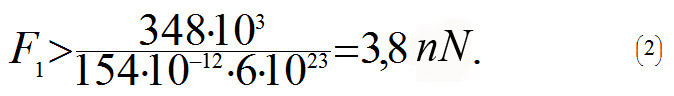
What is the strength of a single-walled nanotube?
From the equation (2) it follows that a nanotube will break when tensile force F is more than 3,8 · N nN, and where N is a number of C-C bonds parallel to the axis in one cross-section plane of the tube. Let us assume that the nanotube's diameter is D = 1.5 nm. Using (1) we get N =18. This is why the nanotube will break when Fmax > 3,8 · 18 nN ≈ 69 nN. In order to calculate the strength σmax of a nanotube, let us divide Fmax by cross-sectional area S= πD2/4:
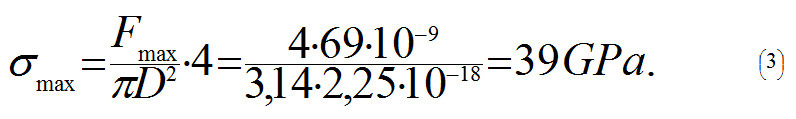
Value σmax which we determine is rather close to maximum values received in experiments (63 GPa), and, as it should have been expected, is a lot stronger than the strongest kinds of steel (0.8 GPa).
Structure's defects, strength and plasticity
An ideal nanotube doesn't have any defects and represents ONE molecule in which carbon atoms are connected to each other with rather strong covalent bonds. Steel is a polycrystalline which has a lot of internal defects - borders and micro-cracks. When stretching a steel, one such defect turns into a crack and the model breaks. The presence of multiple defects explains the ductility of a metal. At the same time a nanotube lacks ductility. If one were to insert one single-walled nanotube into another with a little bit bigger diameter then the strength of such a double-walled nanotube would be twice that of a single-walled. This is why the strength of multi-walled nanotubes is several times greater! Nanotube constructions have a big future. They are, for example, already being used to strengthen tennis rackets. Plans include making ropes out of nanotubes for elevators to supply space stations in geostationary orbits with everything necessary.
Acknowledgement
Content of the web page has been developed by Konstantin Bogdanov. Link to CV. This webpage is an adapted version of the article published in KVANT magazine, (2009, issue 4, p.7) with permission from the Editorial Board.