Symmetry

Symmetry plays a very important role in nature and there is certainly no exception at the atomic scale. Atoms themselves are highly symmetric (spheres) and most of the molecules and all crystalline materials have some elements of symmetry - centers (inversion), axes (rotation), planes (reflection), translation and a general combination of them all. For example, a spiral; a fascinating feature of the DNA molecule, is a combination of rotation around and translation along the symmetry axis.

Each molecule is assigned to a certain point group: a set of symmetry elements which can be applied to this molecule. Completely asymmetric molecules belong to the group C1, which has only one symmetry element: identity (E). Obviously, all other molecules have identity as well and thus all point groups have element E present.

Here are some examples of well known small molecules which have symmetry:

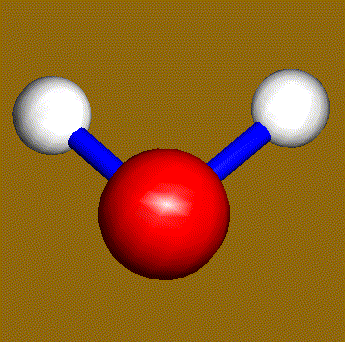
water
 Water(C2v)
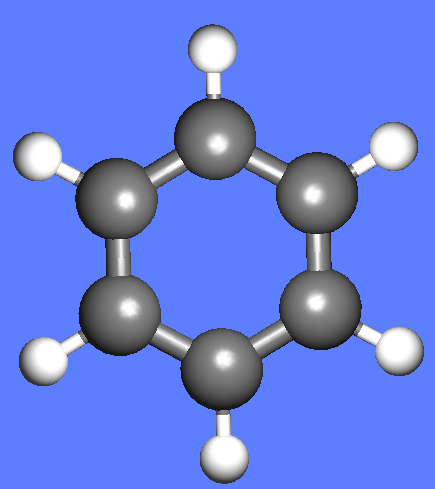
benzene symmetry
 Benzene (D6h )
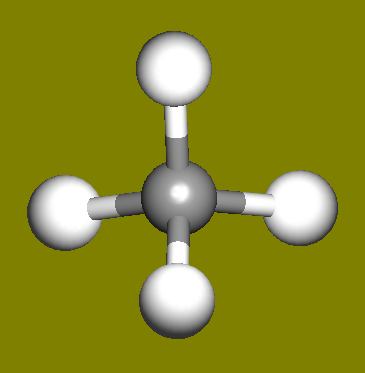
methane
 Methane (Td )
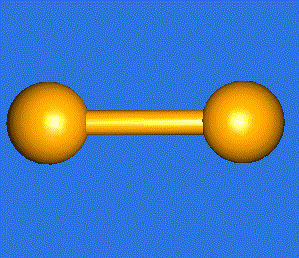
hydrogen
 Hydrogen (D∞h )

The water molecule (H2O) has four symmetry elements: identity (E), 2nd order axis of symmetry (C2) and two symmetry planes (σv). Higher symmetry molecules, such as benzene (C6H6) and methane (CH4), have more elements of symmetry. Methane has five and benzene has twelve different elements of symmetry, while the total number of symmetry elements: twenty four - is equal for both molecules. Hydrogen, a linear molecule with two equivalent atoms, has an infinite number of symmetry elements such as rotations (C2 and C∞), rotation-reflections (S∞) and planes (Cv).

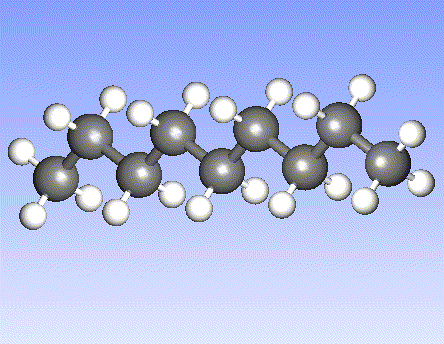
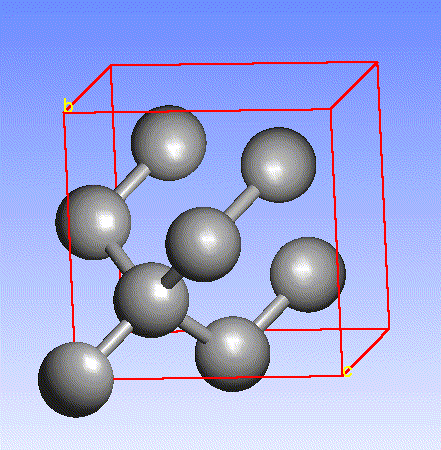
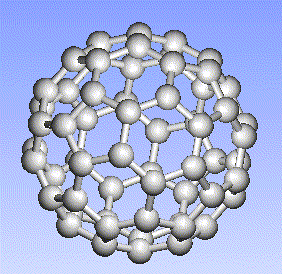
Carbon, the major element in organic molecules, can form linear polymers (such as hydrocarbons (CnHm), two-dimensional sheets (graphite) and three-dimensional crystals (diamond). Fullerenes and nanotubes, which are very popular in nanotechnology research, are also made from carbon as pictured below:

hydrocarbon
 Hydrocarbon
graphite
 Graphite
diamond structure
 Diamond
Fullerene
 Fullerene
Nanotube
 Nanotube

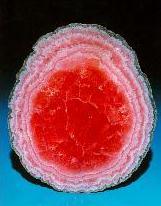
Crystals, macroscopic periodic systems, made from atoms and molecules have fascinating symmetry, which in combination with color is a working horse of the big industry sector - jewelry.Examples of crystals from Steve Smale's collection:

Aquamarine
 Aquamarine
Mesolite
 Mesolite
Rhodochrosite
 Rhodochrosite
Paryte
 Paryte

There are fourteen 3D crystal lattices with different symmetries (Bravais lattices): which are characterized by the relations between unit cell parameters and the presence of the additional lattice point in the center of the unit cell or on its faces. See below:

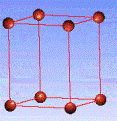
Primitive(P)
Primitive(P)
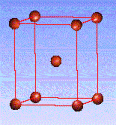
Body-centered(I)
Body-centered(I)
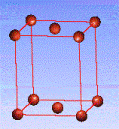
Side-centered(C)
Side-centered(C)
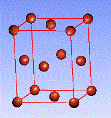
Paryte
Face-centered(F)

There are seven crystal systems which have one or more different types of unite cell (P, I,C, or F):

Crystal system

Unit cell coordinates

Symmetry

Bravais lattices

Cubic

a = b= c;
α = β = γ = 90o

Four 3-fold axes

P, F, I

Tetragonal

a = b ≠ c;
α = β = γ = 90o

One 4-fold axis

P, I

Orthorombic

a ≠ b ≠ c;
α = β = γ = 90o

Three 2-fold axes or mirror planes

P, F, I, C

Hexagonal

a = b ≠ c;
α = β = 90o;
γ = 120o

One 6-fold axis

P

Trigonal

a = b ≠ c;
α = β = 90o;
γ = 120o

One 3-fold axis

P (R)

Monoclinic

a ≠ b ≠ c;
α = β = 90o;
γ ≠ 90o

One 2-fold axis or mirror plane

P, C

Triclinic

a ≠ b ≠ c;
α ≠ β ≠ γ

None

P

There are 230 space groups which are made of 32 crystallographic point groups (crystal classes) compatible with translation symmetry.

 

Acknowledgement

Anatoliy Korkin

This web page is prepared by Anatoli Korkin. Numerous references have been provided by Dr. Inbal Tuvi-Arad. Atomic scale images are created with SageMD2 program and DNA image is created by Anastassia Alexandrova.

More information on molecular and crystal symmetry