Spintronics
Spintronics is a new paradigm for electronics which utilizes the electron's spin in addition to its charge for device functionality. The primary areas for potential applications are information storage, computing, and quantum information. In terms of materials, the study of spin in solids now includes metallic multilayers, inorganic semiconductors, transition metal oxides, organic semiconductors, and carbon nanostructures. The diversity of materials studied for spintronics is a testament to the advances in synthesis, measurement, and interface control that lie at the heart of nano-electronics.
Why spin?
We begin with the question, "What is special about electron spin?" From a scientific and technological point of view, there are four important points. First is the connection between spin and magnetism, which is useful for information storage. Second is an intrinsic connection between spin and quantum mechanics, which may be useful for quantum information. Third is the short range of spin-dependent exchange interactions, which implies that the role of spin will continue to grow as the size of nanostructures continues to shrink. Fourth are the issues of speed and power dissipation, which are becoming increasingly important for electronics at the nanoscale.
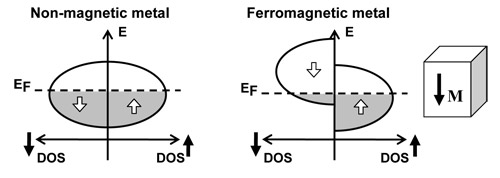
First, spin is connected to ferromagnetic materials because the spontaneous magnetization breaks time-reversal symmetry, which allows the electronic states within the material to become spin-dependent. This contrasts with non-magnetic materials where time-reversal symmetry forces the electronic states to come in pairs with the same energy but opposite spin, thus leading to a density of states that must be independent of spin. In the ferromagnetic metal, the density of states (DOS) is different for the two spin states. It is conventional to refer to the majority spin as "spin up" while the minority spin is "spin down." Because most transport properties depend on the density of states near the Fermi level, the spin asymmetry in the density of states allows ferromagnets to generate, manipulate, and detect spin.
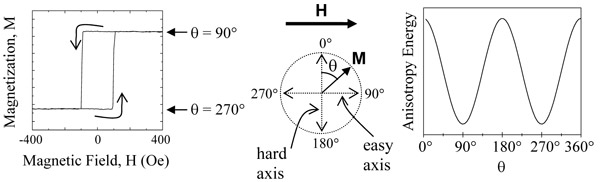
Ferromagnetic materials also possess the property of hysteresis, where the magnetization can have two (or more) different stable states in zero magnetic field. The bistability is due to a property called magnetic anisotropy, where the energy of a system depends on the direction of the magnetization. There is a preferred axis ("easy axis") with stable states for magnetization direction along Ø = 90° and Ø = 270°. When a large magnetic field (H) is applied along an easy axis, the magnetization (M) will align with this field in order to lower the Zeeman energy, EZeeman = - M- H. When the magnetic field is turned off, the magnetization will ideally maintain all of its high-field magnetization.
A magnetic field applied in the opposite direction will cause the magnetization to reverse after the field crosses a value known as the "coercivity" or "coercive field," which depends on the height of the magnetic anisotropy energy barrier. This magnetic anisotropy generally depends on both the material and its shape. In terms of information storage applications, the two stable magnetic states in zero magnetic field correspond to the logical "0" and "1" of a data bit. The data can be written by applying a magnetic field larger than the coercivity to align the magnetization along the field. Due to the anisotropy energy barriers, this state is stable even when the magnetic field is turned off. This property makes ferromagnets natural candidates for information storage. Thus, the connection between spin and ferromagnetism establishes a natural connection between spintronics and information storage applications.
Second, spin is connected to quantum mechanics. In classical mechanics, the angular momentum (i.e. rotational motion) can be divided into two parts, an "orbital" angular momentum and a "spin" angular momentum. If one considers the motion of the earth, the elliptical motion of the earth around the sun generates orbital angular momentum, while the rotation of the earth about its axis generates spin angular momentum. For elementary particles such as the electron, the physics is governed by quantum mechanics. In an atom, the motion of the electron around the nucleus generates orbital angular momentum. The electron also has spin angular momentum, but it is NOT due to a “spinning” motion of the electron. (OK, in a dinner conversation you can describe spin as the spinning motion of an object, but technically this is wrong.)
Instead, spin comes out of quantum mechanics when you try to combine it with special relativity, as Dirac did in the 1920's. In solving the Dirac equation, one of the consequences is the requirement of an internal property that is now known as spin. Because of its intrinsically quantum mechanical origin, it should be of little surprise that the electron spin has very unusual properties. For example, its value along any particular axis (say, the z-axis) can only take on two values: Sz = +ŋ/2 and -ŋ/2. In other notations, these are called "spin up" and "spin down", | ↑ > and , | ↓ > or |m s= ½> and |m s= -½ >. It also obeys a Heisenberg uncertainty principle where the three components of spin ( Sx, Sy, Sz ) cannot be measured simultaneously. Most importantly from the point of view of computing applications, the spin can be in a quantum superposition state, such as A| ↑ >+B| ↓ > where the coefficients A and B are complex numbers.
If you think about digital electronics as being built on bits that can have two states "0" or "1", you can think about spin as a "quantum bit" which can be in states | ↑ > , | ↓ > , or in a superposition state A| ↑ >+B| ↓ >, where |A|2 is the probability of finding the spin in the | ↑ > state and |B|2 is the probability of finding the spin in the | ↓ > state. The quantum bit, or "qubit," lies at the heart of a new type of proposed computer known as a quantum computer which could in principle perform some tasks such as factorizing numbers or performing searches much more efficiently than normal digital computers.
There are many schemes proposed for quantum computing (with most of them being unrelated to electron spin) but there is a debate about whether a scalable quantum computer will ever be realized. Nonetheless, it is a worthy pursuit that pushes the boundaries of our knowledge and technical capabilities, since electron spin presents the opportunity to exploit quantum mechanical behavior in solids in a manner that is generally inaccessible in purely charge-based electronics. It is this special relation between spin and quantum mechanics which forms a natural connection between spintronics and advanced computing, whether the goal is a full-blown quantum computer or a more modest form of quantum information processing that has yet to be devised.
Third, the length scale of spin-dependent exchange interactions is on the order of a few atomic spacings. Because of this, the spin-dependent properties in solids are very sensitive to the atomic scale structure. With the ability to engineer interfaces at the atomic level by growth techniques such as molecular beam epitaxy (MBE), and with the ongoing improvements in the fabrication of smaller and smaller structures in the lateral dimensions, the role of spin is likely to become even more important as nanoscale science continues to advance. Understanding how spin and magnetism depend on the atomic scale interface and material structure will be an important area of investigation for the development of spintronics.
Finally, spintronics has the possibility to deliver high speed performance and low power consumption, although one should be cautious about making such blanket statements. As electronic devices continue to shrink in size, one of the biggest problems is power dissipation and thermal management of circuits. Spin does have some potential benefits in terms of power. In terms of memory, a ferromagnetic bit can store information without any power consumption to maintain the data due to the anisotropy energy barrier (in contrast to some semiconductor memories such as SRAM or DRAM).
In terms of switching, while power is required to generate electrical currents to produce magnetic fields or spin torque, precessional dynamics can ideally proceed without dissipation (although in practice there is always at least a small amount of damping). In the case of magnetization switching by spin torque, this creates a counter-intuitive situation where the critical current required for switching a bit can be lowered by decreasing the damping parameter (e.g. through materials engineering) without decreasing the anisotropy energy barrier which stabilizes the bit. More generally, novel spintronic memory or logic architectures developed in the future may be able to take advantage of precessional dynamics (of magnetization or non-equilibrium spin populations) for low power operation.
These are in principle quite advantageous, but in reality a full power analysis needs to be performed because these energy savings could be more than offset by other required operations (e.g. generating magnetic field pulses, charging up gates, etc.). Spin also has some potential benefits for speed. In charge-based electronics, the speed is set by the RC time constants. In utilizing spin, it may be possible to circumvent this general rule. For example, the precession of spin or magnetism (which can be at high GHz frequencies) is not governed by RC time constants. To sum up, there is potential for high speed, low power applications, but novel circuit architectures need to be developed to bring this to fruition.
Acknowledgement
This web page is an excerpt from the chapter "Fundamentals of Spintronics in Metal and Semiconductor Systems" by Roland Kawakami in the book Nanoelectronics and Photonics: From Atoms to Materials, Devices and Architectures (with permission from the author and the Springer).
Read more about spintronics
YouTube Videos
