Microscopic derivation of zero-flux boundary condition in one-dimensional random walk in presence of a totally reflecting barrier
Marius Orlowski ,
, 
DDL Laboratories, APRDL, Motorola, 3501 Ed Bluestein Boulevard, Austin, TX 78739, USA
Available online 24 June 2003.
Abstract
In this paper a rigorous probabilistic two-probability-parameter model of a diffusion barrier is investigated that describes comprehensively reflection, absorption, and segregation phenomena at a diffusion barrier. As a special case, a rigorous analysis of counting paths for 1D random walk in the presence of a reflecting barrier is presented. This paper defines and makes distinction between partially and totally reflecting barriers. So far, in the literature only a special case of partially reflecting barrier has been dealt with. A combinatorial formula is derived showing that in the presence of a totally reflecting barrier (at mb=0) the probability of a particle departing from position m=2j and arriving at position m=2k on the positive axis after N=2M steps is given by W2j(2k,N) = [C(2M, M-j+k)-C(2M, M-j-k-l)]/[C(2M,M)+2 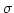 i=0j C(2M,M+i)], where C(n,m) denotes the binomial coefficient. This formula enables easy computation of any random walk redistribution of a diffusing species near or at the totally reflecting barrier. The analysis shows that for a particle starting its random walk at the barrier, the probability of finding it at the interface is diminishing with the number of diffusion steps N=2M as 1/(M+1) and that the peak of the probability distribution is moving away from the barrier with the increasing number of steps as
i=0j C(2M,M+i)], where C(n,m) denotes the binomial coefficient. This formula enables easy computation of any random walk redistribution of a diffusing species near or at the totally reflecting barrier. The analysis shows that for a particle starting its random walk at the barrier, the probability of finding it at the interface is diminishing with the number of diffusion steps N=2M as 1/(M+1) and that the peak of the probability distribution is moving away from the barrier with the increasing number of steps as  . Thus, the subsurface region is progressively depleted. The present analysis has bearing on the treatment of diffusion of impurities and point defects in thin films and in subsurface layers.
. Thus, the subsurface region is progressively depleted. The present analysis has bearing on the treatment of diffusion of impurities and point defects in thin films and in subsurface layers.

 Corresponding author. Fax: +1-512-933-5304.
Corresponding author. Fax: +1-512-933-5304.


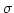 i=0j C(2M,M+i)], where C(n,m) denotes the binomial coefficient. This formula enables easy computation of any random walk redistribution of a diffusing species near or at the totally reflecting barrier. The analysis shows that for a particle starting its random walk at the barrier, the probability of finding it at the interface is diminishing with the number of diffusion steps N=2M as 1/(M+1) and that the peak of the probability distribution is moving away from the barrier with the increasing number of steps as
i=0j C(2M,M+i)], where C(n,m) denotes the binomial coefficient. This formula enables easy computation of any random walk redistribution of a diffusing species near or at the totally reflecting barrier. The analysis shows that for a particle starting its random walk at the barrier, the probability of finding it at the interface is diminishing with the number of diffusion steps N=2M as 1/(M+1) and that the peak of the probability distribution is moving away from the barrier with the increasing number of steps as